Πρόσθεση ακεραίων

Όσο κι αν η πρόσθεση φαίνεται η ευκολότερη πράξη, είναι πολύ βασικό να μάθουμε να την εκτελούμε σωστά, γιατί θα τη συναντήσουμε σε πολλά προβλήματα τόσο στο σχολείο όσο όμως και στην καθημερινότητά μας, π.χ. στο σούπερ μάρκετ, στο μαγαζί με τα παιχνίδια κλπ.

Ας ξεκινήσουμε από την αρχή. Μάθαμε στην προηγούμενη τάξη ότι οι αριθμοί διακρίνονται σε μονάδες, δεκάδες, εκατοντάδες, χιλιάδες κ.ο.κ. Ο αριθμός για παράδειγμα 156 αναλύεται όπως φαίνεται παρακάτω:

εκατοντάδες	δεκάδες	μονάδες
1	5	6

ή διαφορετικά 156 = 100 + 50 + 6

Βασικός και απαράβατος κανόνας που πρέπει να θυμόμαστε πάντα είναι ότι όταν έχουμε να προσθέσουμε δύο αριθμούς, προσθέτουμε τα όμοια ψηφία, δηλαδή τις μονάδες με τις μονάδες, τις δεκάδες με τις δεκάδες κλπ. Διαφορετικά θα προκύψει λάθος αποτέλεσμα.

Ας το δούμε στην πράξη σε ένα παράδειγμα:

Έστω ότι μας δίνουν την πρόσθεση 156 + 32. Σύμφωνα με όσα είπαμε παραπάνω θα έχουμε:

156 + 32 = (100 + 50 + 6) + (30 + 2) = 100 + (50 + 30) + (6 + 2) = 100 + 80 + 8 = 188

                                                                                             Δεκάδες    Μονάδες      

Βέβαια αυτό στην περίπτωση που έχουμε να κάνουμε με μικρούς σχετικά αριθμούς είναι εφικτό. Όταν όμως οι αριθμοί είναι μεγαλύτεροι είναι δύσκολο και χρονοβόρο να κάνουμε όλη την παραπάνω διαδικασία. Γι αυτές τις περιπτώσεις, αλλά και για να κάνουμε την πρόσθεση πιο εύκολη γενικώς, καταφεύγουμε στην κάθετη πράξη, τοποθετώντας τους δύο αριθμούς έτσι ώστε οι μονάδες να βρίσκονται κάτω από τις μονάδες, οι δεκάδες κάτω από τις δεκάδες κ.ο.κ. Ευνόητο είναι πως όπου δεν υπάρχει κάποιο ψηφίο, εννοείται το μηδέν (0).

εκατοντάδες	δεκάδες	μονάδες
1	5	6
+	3	2
-----------------------------------
1	8	8

Μέχρι εδώ καλά. Πολλές φορές όμως το αποτέλεσμα της άθροισης στα επιμέρους κομμάτια βγαίνει μεγαλύτερο από δέκα. Τότε έχουμε το λεγόμενο «κρατούμενο». Τι είναι όμως αυτό; Πολύ απλά, είναι η δεκάδα ή εκατοντάδα ή χιλιάδα κλπ που προκύπτει από την πρόσθεση και την οποία προσθέτουμε στην επόμενη βαθμίδα, όπου και ανήκει. Ας δούμε ένα παράδειγμα, 635 + 79

635 + 79 = (600+30+5) + (70+9) = 600 + (30+70) + (5+9) =

                                                                                      Δεκάδες  Μονάδες

600 + 100 + 14 = (600+100) + 10 + 4 = 700 + 10 + 4 = 714

                                           

Βλέπουμε λοιπόν ότι το άθροισμα των δεκάδων είναι 100, άρα μία εκατοντάδα η οποία θα προστεθεί στις όμοιες της, ενώ το άθροισμα των μονάδων είναι 14, άρα 1 δεκάδα και 4 μονάδες.

Πάμε να το δούμε στην κάθετη πράξη.

εκατοντάδες	δεκάδες	μονάδες
6	3	5
+	7	9
-----------------------------------
7	1	4

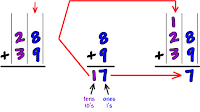
Βήμα πρώτο: 9+5 = 14, άρα γράφουμε το 4 και το 1 (την δεκάδα που προκύπτει δηλαδή την έχουμε ως κρατούμενο)

Βήμα δεύτερο: 7+3 = 10 + 1 (κρατούμενο) = 11, άρα γράφουμε το 1 και το 1 (την εκατοντάδα δηλαδή που προέκυψε) την κρατούμε για τη συνέχεια.

Βήμα τρίτο: 6 + 0 = 6 + 1 (κρατούμενο) = 7

Επομένως το άθροισμα που προκύπτει είναι το 714... 

Για εξάσκηση παίζοντας πατήστε ΕΔΩ

Μιλτιάδης Ζωγράφος